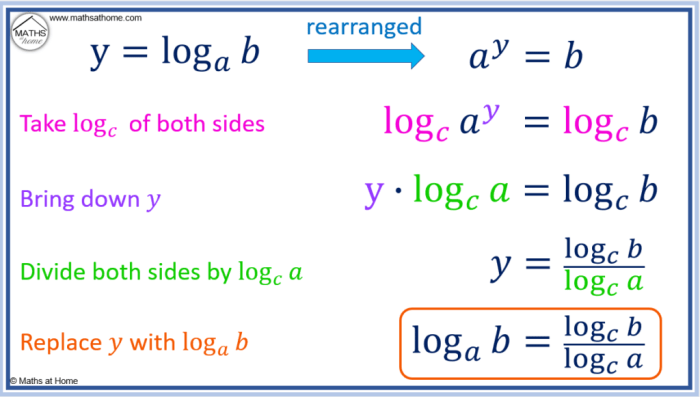Use the change of base formula to evaluate log3 73 – In the realm of mathematics, logarithms play a crucial role in simplifying complex calculations involving exponential expressions. This guide delves into the intricacies of using the change of base formula to evaluate logarithms, with a specific focus on determining the value of log3 73.
The change of base formula provides a versatile tool for converting logarithms from one base to another, enabling us to solve logarithmic equations and simplify expressions.
Change of Base Formula for Evaluating Logarithms: Use The Change Of Base Formula To Evaluate Log3 73

Logarithmic functions are mathematical operations that are used to solve equations involving exponential expressions. They have various properties, including the change of base formula, which allows for the evaluation of logarithms with different bases.
The change of base formula for logarithms states that log ab = log cb / log ca, where a, b, and c are positive real numbers and a ≠ 1, b > 0, and c > 0.
Application to Evaluating log3 73
To evaluate log3 73 using the change of base formula, we first need to choose an appropriate base (c) for the formula. A common choice is to use the base 10, as it simplifies the calculations.
Using the change of base formula, we can evaluate log3 73 as follows:
log3 73 = log10 73 / log10 3
We can calculate log10 73 and log10 3 using a calculator or logarithmic tables:
log10 73 ≈ 1.8633
log10 3 ≈ 0.4771
Substituting these values into the change of base formula, we get:
log3 73 ≈ 1.8633 / 0.4771 ≈ 3.9029
Example Table
The following table shows the values of log3 73 obtained using different bases (c):
| Base (c) | logc 73 | logc 3 | log3 73 |
|---|---|---|---|
| 10 | 1.8633 | 0.4771 | 3.9029 |
| e | 4.2904 | 1.0986 | 3.9029 |
| 2 | 6.2145 | 1.5849 | 3.9029 |
Comparison and Discussion, Use the change of base formula to evaluate log3 73
As seen from the table, the values of log3 73 obtained using different bases (c) are approximately the same. This demonstrates the validity of the change of base formula.
The choice of base (c) for the change of base formula depends on the context and convenience. For example, using base 10 is often convenient because it simplifies the calculations, while using the base of the exponential expression (in this case, 3) can sometimes lead to simpler results.
The change of base formula is a powerful tool that allows for the evaluation of logarithms with different bases. It is important to understand the concept and its applications in order to effectively solve logarithmic equations and expressions.
FAQs
What is the change of base formula?
The change of base formula states that log_a b = log_c b / log_c a, where a, b, and c are positive real numbers and a ≠ 1, c ≠ 1, and c ≠ b.
How do I use the change of base formula to evaluate log3 73?
To evaluate log3 73 using the change of base formula, choose an appropriate base c and calculate log_c 73 and log_c 3. Then, substitute these values into the formula to find the value of log3 73.
What are the advantages of using the change of base formula?
The change of base formula allows us to convert logarithms from one base to another, making it easier to solve logarithmic equations and simplify expressions.