Embark on an intellectual journey through Unit 1 Equations and Inequalities Homework 2, a comprehensive exploration of foundational algebraic concepts. This assignment delves into the intricate world of equations and inequalities, equipping students with essential problem-solving skills and a deeper understanding of mathematical relationships.
From the fundamental principles of equations to the nuances of inequality representation, this homework assignment provides a structured framework for mastering these algebraic building blocks. By engaging in a series of carefully crafted exercises and assessments, students will refine their ability to solve equations, manipulate inequalities, and apply these concepts to real-world scenarios.
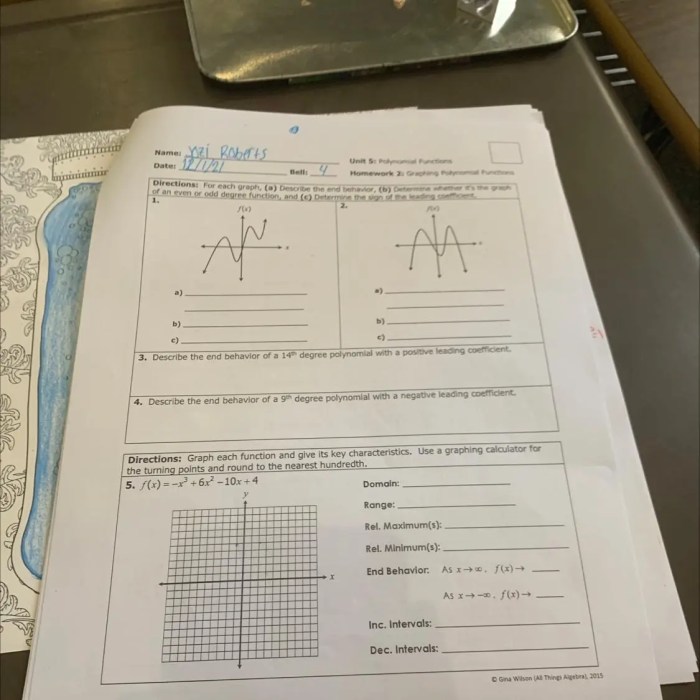
Equations and Inequalities

Equations and inequalities are fundamental mathematical concepts that are widely used in various fields of study and everyday life. Understanding these concepts is crucial for solving problems, making informed decisions, and analyzing data.
Equations
An equation is a mathematical statement that establishes the equality of two expressions. It consists of two sides, separated by an equal sign (=). The expressions on both sides of the equation have the same value.
There are different types of equations, including:
- Linear equations: Equations that can be written in the form ax + b = c, where a, b, and c are constants.
- Quadratic equations: Equations that can be written in the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0.
li>Polynomial equations: Equations that involve polynomials, which are expressions consisting of variables and constants.
Solving equations involves isolating the variable on one side of the equation and finding the value that makes the equation true.
Inequalities
An inequality is a mathematical statement that establishes a relationship between two expressions that are not equal. Inequalities are represented using symbols such as <, >, ≤, and ≥.
There are two types of inequalities:
- Strict inequalities: Inequalities that use the symbols < or >, indicating that one expression is strictly less than or greater than the other.
- Non-strict inequalities: Inequalities that use the symbols ≤ or ≥, indicating that one expression is less than or equal to, or greater than or equal to, the other.
Solving inequalities involves isolating the variable and finding the values that satisfy the inequality.
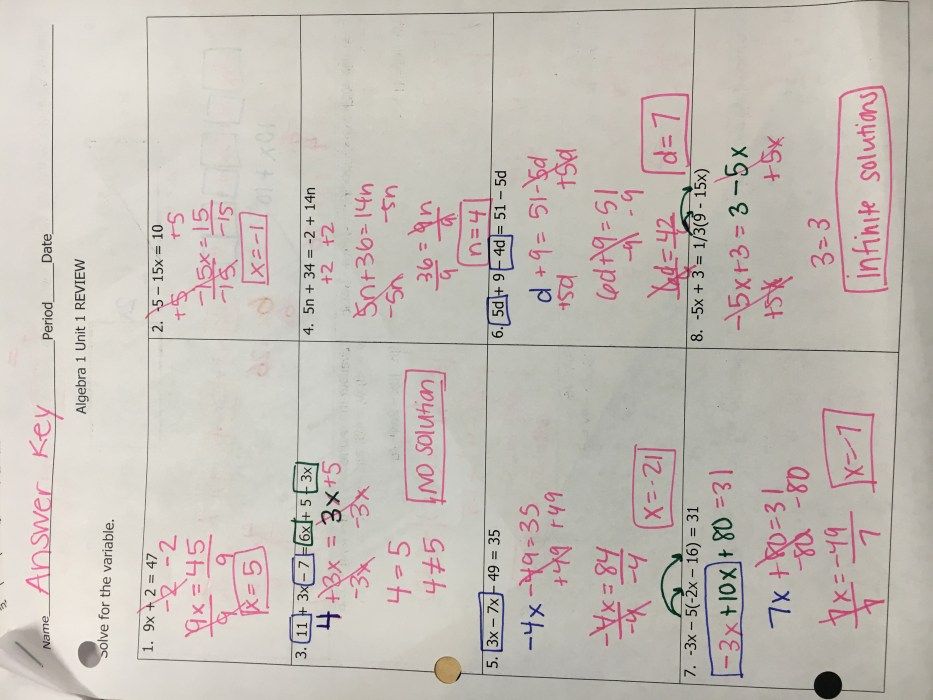
Solving Equations and Inequalities, Unit 1 equations and inequalities homework 2
Solving equations and inequalities involves using algebraic operations to isolate the variable and find the values that make the statement true. Common methods include:
- Adding or subtracting the same value to both sides
- Multiplying or dividing both sides by the same non-zero value
- Using inverse operations, such as squaring or taking the square root
Solving compound inequalities and inequalities with absolute values requires additional techniques and understanding of the properties of inequalities.
Applications of Equations and Inequalities
Equations and inequalities have numerous applications in various fields, including:
- Physics: Describing motion, forces, and energy
- Chemistry: Balancing chemical equations and determining concentrations
- Economics: Modeling supply and demand, and optimizing production
- Everyday life: Solving problems related to finance, time management, and decision-making
Understanding equations and inequalities is essential for problem-solving, data analysis, and making informed decisions in both academic and real-world contexts.
Frequently Asked Questions: Unit 1 Equations And Inequalities Homework 2
What are the different types of equations?
Equations can be classified into various types, including linear equations, quadratic equations, exponential equations, and logarithmic equations, each with its unique structure and solution methods.
How do you solve inequalities with absolute values?
Solving inequalities with absolute values involves isolating the absolute value expression and considering two cases: one where the expression is positive and the other where it is negative. By solving each case separately, you can determine the solution set of the inequality.
What are the applications of equations and inequalities in real-life situations?
Equations and inequalities find widespread applications in various fields, such as physics, engineering, economics, and finance. They are used to model physical phenomena, optimize resource allocation, and make informed decisions based on mathematical relationships.